Lösungen zur Scheitelpunktform
Inhaltsverzeichnis
\(\\\)
Lösungen zur Scheitelpunktform bei einer verschobenen Normalparabel
Lösung 1
Von der allgemeinen Form zur Scheitelpunktform:
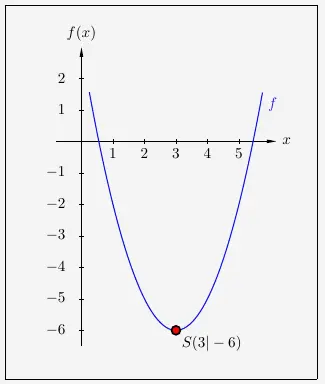
\( \quad \begin{array}{ r c l } f(x) & = & x^2 - 6x + 3 \\[5pt] f(x) & = & x^2 - 6x + 3^2 - 3^2 + 3 \\[5pt] f(x) & = & (x - 3)^2 - 9 + 3 \\[5pt] f(x) & = & (x - 3)^2 - 6 \\ \end{array} \)
\(\\\)
Es ergibt sich folgender Scheitelpunkt, hier mit dem dazugehörigen Graphen:
\(\\[1em]\)
Lösung 2
Von der allgemeinen Form zur Scheitelpunktform:
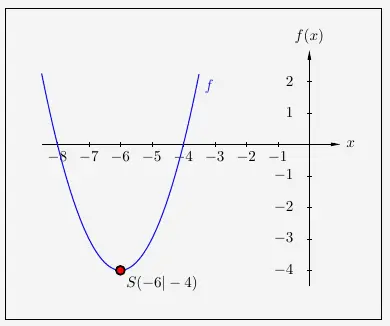
\( \quad \begin{array}{ r c l } f(x) & = & x^2 + 12x + 32 \\[5pt] f(x) & = & x^2 + 12x + 6^2 - 6^2 + 32 \\[5pt] f(x) & = & (x + 6)^2 - 36 + 32 \\[5pt] f(x) & = & (x + 6)^2 - 4 \\ \end{array} \)
\(\\\)
Es ergibt sich folgender Scheitelpunkt, hier mit dem dazugehörigen Graphen:
\(\\[1em]\)
Lösung 3
Von der allgemeinen Form zur Scheitelpunktform:
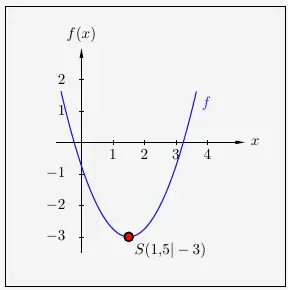
\( \quad \begin{array}{ r c l } f(x) & = & x^2 - 3x - 0{,}75 \\[5pt] f(x) & = & x^2 - 3x + 1{,}5^2 - 1{,}5^2 - 0{,}75 \\[5pt] f(x) & = & (x - 1{,}5)^2 - 2{,}25 - 0{,}75 \\[5pt] f(x) & = & (x - 1{,}5)^2 - 3 \\ \end{array} \)
\(\\\)
Es ergibt sich folgender Scheitelpunkt, hier mit dem dazugehörigen Graphen:
\(\\[2em]\)
Lösungen zur Scheitelpunktform bei einer gestreckten Parabel
Lösung 1
Von der allgemeinen Form zur Scheitelpunktform:
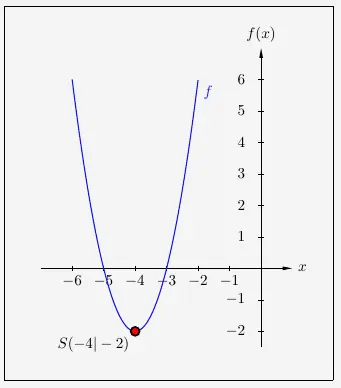
\( \quad \begin{array}{ r c l } f(x) & = & 2x^2 + 16x + 30 \\[5pt] f(x) & = & 2 \cdot \left( x^2 + 8x \right) + 30 \\[5pt] f(x) & = & 2 \cdot \left( x^2 + 8x + 4^2 - 4^2 \right) + 30 \\[5pt] f(x) & = & 2 \cdot \left( (x + 4)^2 - 16 \right) + 30 \\[5pt] f(x) & = & 2 \cdot (x + 4)^2 - 2 \cdot 16 + 30 \\[5pt] f(x) & = & 2 \cdot (x + 4)^2 - 2 \\ \end{array} \)
\(\\\)
Es ergibt sich folgender Scheitelpunkt, hier mit dem dazugehörigen Graphen:
\(\\[1em]\)
Lösung 2
Von der allgemeinen Form zur Scheitelpunktform:
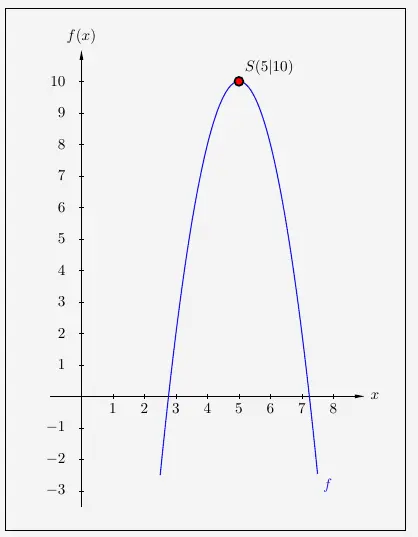
\( \quad \begin{array}{ r c l } f(x) & = & -2x^2 + 20x -40 \\[5pt] f(x) & = & -2 \cdot \left( x^2 - 10x \right) - 40 \\[5pt] f(x) & = & -2 \cdot \left( x^2 - 10x + 5^2 - 5^2 \right) - 40 \\[5pt] f(x) & = & -2 \cdot \left( (x - 5)^2 - 25 \right) - 40 \\[5pt] f(x) & = & -2 \cdot (x - 5)^2 + 2 \cdot 25 - 40 \\[5pt] f(x) & = & -2 \cdot (x - 5)^2 + 10 \\ \end{array} \)
\(\\\)
Es ergibt sich folgender Scheitelpunkt, hier mit dem dazugehörigen Graphen:
\(\\[2em]\)
Lösungen zur Scheitelpunktform mit Brüchen
Lösung 1
Von der allgemeinen Form zur Scheitelpunktform:
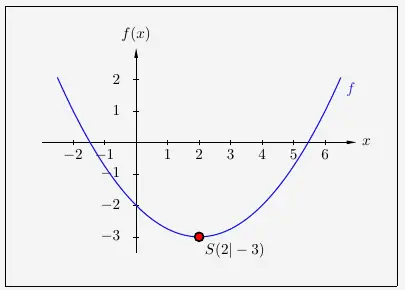
\( \quad \begin{array}{ r c l } f(x) & = & \frac{1}{4}x^2 - x - 2 \\[5pt] f(x) & = & \frac{1}{4} \cdot \left( x^2 - \frac{4}{1} \cdot x \right) - 2 \\[6pt] f(x) & = & \frac{1}{4} \cdot \left( x^2 - 4x + 2^2 - 2^2 \right) - 2 \\[6pt] f(x) & = & \frac{1}{4} \cdot \left( (x - 2)^2 - 4 \right) -2 \\[6pt] f(x) & = & \frac{1}{4} \cdot (x - 2)^2 - \frac{4}{1} \cdot 4 - 2 \\[6pt] f(x) & = & \frac{1}{4} \cdot (x - 2)^2 - 3 \\ \end{array} \)
\(\\\)
Es ergibt sich folgender Scheitelpunkt, hier mit dem dazugehörigen Graphen:
\(\\[1em]\)
Lösung 2
Von der allgemeinen Form zur Scheitelpunktform:
\( \quad \begin{array}{ r c l } f(x) & = & \frac{1}{6}x^2 + \frac{1}{3}x -\frac{7}{3} \\[8pt] f(x) & = & \frac{1}{6} \cdot \left( x^2 + \frac{6}{1} \cdot \frac{1}{3} x \right) -\frac{7}{3} \\[8pt] f(x) & = & \frac{1}{6} \cdot \left( x^2 + \frac{6}{3} x \right) -\frac{7}{3} \\[8pt] f(x) & = & \frac{1}{6} \cdot \left( x^2 + 2x \right) -\frac{7}{3} \\[8pt] f(x) & = & \frac{1}{6} \cdot \left( x^2 + 2x + 1^2 - 1^2 \right) -\frac{7}{3} \\[8pt] f(x) & = & \frac{1}{6} \cdot \left( (x + 1)^2 - 1 \right) -\frac{7}{3} \\[8pt] f(x) & = & \frac{1}{6} \cdot (x + 1)^2 - \frac{1}{6} \cdot 1 -\frac{7}{3} \\[8pt] f(x) & = & \frac{1}{6} \cdot (x + 1)^2 - \frac{1}{6} \cdot 1 -\frac{14}{6} \\[8pt] f(x) & = & \frac{1}{6} \cdot (x + 1)^2 -\frac{15}{6} \\[8pt] f(x) & = & \frac{1}{6} \cdot (x + 1)^2 -2{,}5 \\ \end{array} \)
\(\\\)
Es ergibt sich folgender Scheitelpunkt, hier mit dem dazugehörigen Graphen:

\(\\[1em]\)
Lösung 3
Von der allgemeinen Form zur Scheitelpunktform:
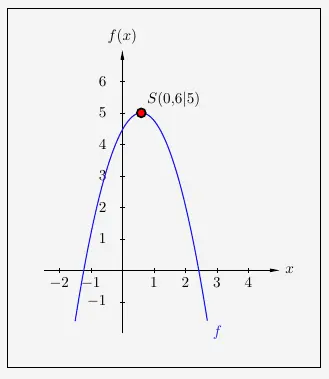
\( \quad \begin{array}{ r c l } f(x) & = & -\frac{3}{2}x^2 + \frac{9}{5}x +\frac{223}{50} \\[8pt] f(x) & = & -\frac{3}{2} \cdot \left( x^2 - \frac{2}{3} \cdot \frac{9}{5} x \right) +\frac{223}{50} \\[12pt] f(x) & = & -\frac{3}{2} \cdot \left( x^2 - \frac{18}{15} x \right) +\frac{223}{50} \\[12pt] f(x) & = & -\frac{3}{2} \cdot \left( x^2 - \frac{6}{5}x \right) +\frac{223}{50} \\[10pt] f(x) & = & -\frac{3}{2} \cdot \left( x^2 - \frac{6}{5}x + \left(\frac{3}{5}\right)^2 - \left(\frac{3}{5}\right)^2 \right) +\frac{223}{50} \\[10pt] f(x) & = & -\frac{3}{2} \cdot \left( \left(x^2-\frac{3}{5}\right)^2 - \frac{9}{25} \right)+\frac{223}{50} \\[8pt] f(x) & = & -\frac{3}{2} \cdot \left(x^2-\frac{3}{5}\right)^2 + \frac{3}{2} \cdot \frac{9}{25} +\frac{223}{50} \\[8pt] f(x) & = & -\frac{3}{2} \cdot \left(x^2-\frac{3}{5}\right)^2 + \frac{27}{50} +\frac{223}{50} \\[8pt] f(x) & = & -\frac{3}{2} \cdot \left(x^2-\frac{3}{5}\right)^2 +\frac{250}{50} \\[8pt] f(x) & = & -\frac{3}{2} \cdot \left(x^2-0{,}6\right)^2 +5 \\ \end{array} \)
\(\\\)
Es ergibt sich folgender Scheitelpunkt, hier mit dem dazugehörigen Graphen:
\(\\[2em]\)
Lösungen zu Nullstellen bei der Scheitelpunktform
Lösung 1
Bedingung: \(f(x)=0\)
\(\\\)
\( \quad \begin{array}{ r c l l c r c l l } (x + 1)^2 - 4 & = & 0 & | + 4 \\[5pt] (x + 1)^2 & = & 4 & | \sqrt{\cdots} \\[5pt] x + 1 & = & -2 & | - 1 & \quad \textrm{und} & \quad x + 1 & = & 2 & | - 1 \\[5pt] x_1 & = & - 3 & & & x_2 & = & 1 & \\ \end{array} \)
\(\\\)
graphisch dargestellt:

\(\\[1em]\)
Lösung 2
Bedingung: \(f(x)=0\)
\(\\\)
\( \quad \begin{array}{ r c l l c r c l l } -\frac{2}{3}(x - 2)^2 + 6 & = & 0 & | - 6 \\[5pt] -\frac{2}{3}(x - 2)^2 & = & - 6 & | \cdot \left( -\frac{3}{2} \right) \\[5pt] (x - 2)^2 & = & 6 \cdot \frac{3}{2} & \\[5pt] (x - 2)^2 & = & 9 & | \sqrt{\cdots} \\[5pt] x - 2 & = & -3 & | + 2 & \quad \textrm{und} & \quad x - 2 & = & 3 & | + 2 \\[5pt] x_1 & = & - 1 & & & x_2 & = & 5 & \\ \end{array} \)
\(\\\)
graphisch dargestellt:

\(\\[1em]\)